TYPES OF FOURIER TRANSFORMS

It is assumed that the function f(t) has a Fourier transfer, i.e., that f(t) satisfies various conditions (finite number of finite discontinuities, absolutely integrable). The type of functions encountered in experimental work almost always have transforms, so we will not go any further into the requirements for transforms to exist.

Types of Fourier Transforms

Fourier Series - If the function f(x) is periodic, then the expression of f(x) as a series of frequency terms with varying terms can be performed with discrete frequencies, though perhaps with an infinite number of terms.

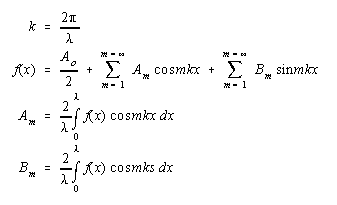
If f(x) is an even function, only cosine terms exist, if f(x) is odd, only sine terms exist.

Fourier Integral - If the function is not periodic, then use integrals with limits of infinity

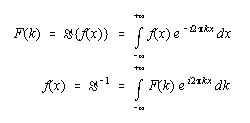
Discrete Fourier Transform - for computer calculations, continuous integrals must be replaced by discrete sums, using a finite number N of data samples taken with a temporal spacing of T seconds apart (here using a time series instead of data sampling over a spatial region). Note that k is simply an integer counter, k = 0, 1, 2, ... , N-1.

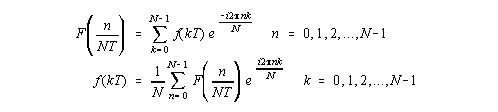
However, these equations are frequently impractical, since the number of calculations is proportional to N², and when N gets large even powerful computers cannot produce results in a reasonable time.

Fast Fourier Transform

In order to get around the calculational expense of the standard form of the discrete Fourier transform (DFT), Cooley and Tukey (1965) figured out how to remove much of the redundancy in the above equations and came up with what is now known as the Fast Fourier Transform (FFT). The FFT is not a simple equation, but an algorithm which allows the Fourier transform of discrete data sets in N log₂ N steps, instead of N². Note that certain errors creep into the calculation because of discretizing the data, but they are found in all DFTs. The FFT is merely one particularly efficient methed of calculating a DFT and introduces no additional error. Note also that the data sampling rate must satisfy the Nyquist Theorem.

Send Mail: matthysd@vms.csd.mu.edu

Visitors to this page :