Feb
5, 2001
Noise
Common
types of noise found in images:
1.
Uniform (white) noise:
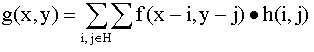
2.
Gaussian noise:
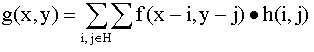
where
m is the mean and σ is the standard deviation.
3.
Negative exponential noise:
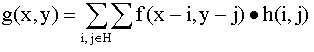
4.
Salt-and-Pepper noise:
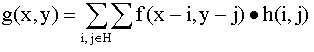

Spatial
Filters
Convolution
of an NxM f(x,y) image with a filter impulse response h(x,y) defined over the
set of elements given by H is given by:
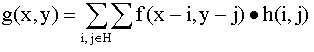
where
0 ≤ x-i < N and
0 ≤ y-j < M

Low
Pass Filters
1.
Mean (or average) filter
(3x3):
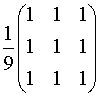
This
filter works fairly well for Gaussian noise, is poor for salt-and-pepper noise,
and has the side-effect of reducing high frequencies. It is basically a low-pass filter.
The larger the size of the filter, the more pronounced its effects.
2.
Gaussian filter with
a = 3.32:
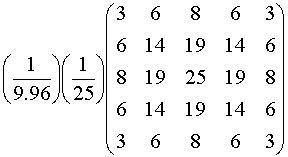
The
values of the above filter are calculated from
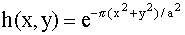
The
constants in front are the normalizing constants to make the sum of all the
coefficients equal to unity.

High-Pass
Filters
It
is more difficult to get a high-pass filter than a low-pass filter.
Indeed, to get a high-pass filter, the general procedure is to apply a
low-pass filter to the original image and then subtract this low-frequency image
from the original image. The result
is then an image containing only high frequencies. Sometimes it is desired
to enhance the high frequencies without removing the low frequencies.
This is called giving the image a high-frequency boost.
This can be done by using a gain factor G (usually between 0 and 2) and
following the procedure involved in:
fh(x,y)
= f(x,y) + G • [f(x,y) - fmean(x,y)] = (1 + G)•f(x,y) - G•fmean(x,y)
Example
of High-Pass filter with boost:
start
with identity filter:

after
subtracting a mean filter:
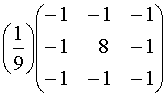
add
gain G (range 0 to2):
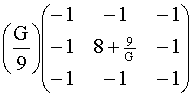

Rank
Order Filtering
Median
filter:
This
type of filter is much better at removing outlier type noise such as
salt-and-pepper and does not reduce high frequencies as much as the mean filter.
It does not use convolution, but instead is one of a class of filters
called rank filters, that ranks the values of the neighbors of a specified
pixel, and inserts the median value of the neighboring pixels at the location of
the specified pixel.
Example:
Original
image with sharp edge and one outlier:
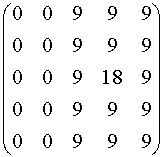
Image
after filtering with a median filter:

Image
after filtering with a mean filter:
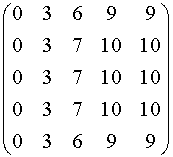

Derivative
Filters
Averaging
pixels blurs detail in an image, since averaging filters are basically low-pass
filters. This averaging is similar
to integration where everything is just summed up. On the other hand, if it is desired to enhance rapid change
(high frequencies) rather than slow change (low frequencies), some sort of
differentiation operation must be developed.
The
gradient function is used to determine the direction of change in a vector.
For a two-dimensional image, this could be expressed in vector form as:
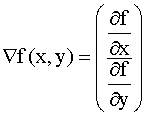
The
magnitude of the gradient is
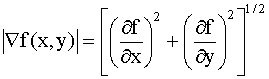
In
terms of images, consider the pixels under a 3x3 mask:
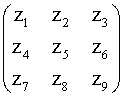
To
get derivatives in the x and y directions at z5,
one simple method is to take differences
such
as (z6 - z5), to ignore the squaring and root-taking of
the definition of the magnitude of the gradient, and simply to approximate
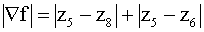
However,
using masks of even size 2x2 is awkward, so more commonly a 3x3 neighborhood is
used, giving
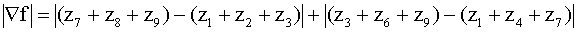
This
approximation is expressed in the following two masks for the x and y
directions, respectively, which are called Prewitt operators:
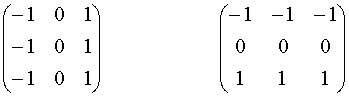
Another
common approximation to the magnitude of the gradient is given by the Sobel
operators for x and y directions, respectively:

All
of these derivative operators accentuate rapid change (edges) in the image and
attenuate large objects. They are
frequently used as edge detectors.
Last modified on February 13, 2001
