Instead of using filter mask, can work in the frequency space using the convolution theorem. Application of the mask to each pixel (x,y) is basically a convolution process, so can get same results by multiplying the Fourier transforms of the image and the mask and then inverse Fourier transforming the product. The reason for this approach is that it is sometimes much easier to specify the filter in frequency space, and for masks of modest size (e.g. 7x7 or larger) it is faster to work with the Fourier transforms.

In determining H(n,m) the transfer function which corresponds to h(x,y), the impulse function, the need to preserve phase requires that H(n,m) be real, i.e., no imaginary components. This implies that the inpulse function is symmetric: h(x,y) = h(-x,-y).

In the interest of simplicity, the discussion here will assume circular symmetry, that is, H(n,m) => H(ρ) where ρ² = n² + m².

The ideal low-pass filter (ILPF) passes without attenuation all frequencies below some cutoff frequency(f_c) and attenuates to zero all frequencies above f_c. The problem with this is that it introduces a discontinuity into the frequency spectrum and thus causes ringing effects (artifacts) in image space.

A more realistic approach is to use a Butterworth low-pass filter (BLPF) which gives a continuous and monotonic response without discontinuity and without ripples in the frequency domain. The equation for a BLPF is given by:

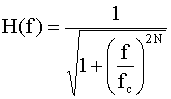
where N is the order of the filter (the larger the order, the sharper the cutoff with be; the order is determined by the number of reactors [capacitors and inductors] in the circuit).

The Butterworth high-pass filter is similar, the only difference is that the fraction in the denominator is inverted:

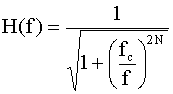
If circularly symmetric filters are being used,  the image data must be moved to the center of the two-dimensional Fourier NxM space by multiplying each element (x,y) in the image by (-1)^x+y, and the zero of frequency space must be shifted by

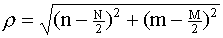
Do Assignment 4.

Last modified on February 07, 2001