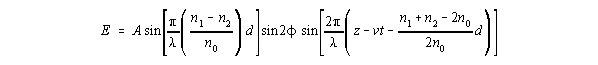
Previous discussion centered on isochromatic fringes, i.e., fringes caused by the extinction of various wavelengths or colors when polychromatic light is passed through birefringent material. If the birefringence is linearly related to the stresses in the material, these fringes can be used to calculate the intensity of (s1 - s2), or equivalently the maximum shear stress, at any point in the field of view. It is, however, difficult to interpret the colored fringe pattern when it results from polychromatic light. The overlap of wavelengths in different orders causes the pattern repetition to be hard to observe, since the colors do not repeat uniformly. This problem can be mitigated by the use of monochromatic light, especially light of the wavelength equal to the so-called tint-of-passage. In this case, sharp narrow fringes can be seen and easily counted.
However, these isochromatic fringes only give the magnitude of stress over the field. Stress is a vector, and so it is necessary to determine the direction of the stress at each point. This determination requires a different set of fringes, called isoclinic fringes. To understand these fringes, it is necessary to consider the basic equation for a linear dark-field polariscope:
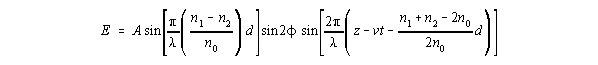
Here E is the monochromatic light wave amplitude emerging from the linear dark-field polarizer, f is the angle between the orthogonal axes of the birefringent material and the axes of the polarizer/analyzer pair, n1 and n2 are the two refractive indicies of the material, n0 is the index of the surrounding medium (almost always air), d is the thickness of the birefringent model, and v is the velocity of light in the model. It is assumed that the coordinate axes of the model are chosen with z along the direction of light flow, and x and y two orthogonal directions in the plane of the model. Frequently the x-axis is taken to be along the direction of the applied load.
Looking at the first two sine terms, it is clear that there are two conditions under which light transmission will be cancelled:
Cancellation Fringes due to the first cause are called isoclinics, while those resulting from the second cause are isochromatics.
It is by using the isoclinics that the direction of the stress can be determined. If the polarizers are rotated slowly, all the points on the image where the birefringent axes are aligned with the polarizer/analyzer axes turn black (the isoclinics). Thus rotating the polarizers and watching the isoclinics will show the direction of the stress components everywhere over the image. Note that the isoclinics are always black and will move over the image when the polarizers are rotated.
It is thus by using both the isoclinics and the isochromatics that the direction and magnitude of the stress at any point can be determined.
![]()
Detailed background material at a lower mathematical level than the course text can be found in Dally and Riley, Experimental Stress Analysis. Cf. Chapter 10: section 6, Chapter 12: sections 1-6, and Chapter 13: sections 1-4.
![]()
Last Modified on April 20, 1997