CIRCULAR POLARISCOPE

Quarter-Wave Plates

A common enhancement to the linear polariscope described previously is the addition of a pair of quarter-wave plates, inserted with their fast and slow axes crossed and oriented with their axes at 45 degrees with respect to the polarizers. Such an arrangement produces what is called a circular polariscope, because the effect of the quarter-wave plates is to produce circularly polarized light between the polarizers. Assuming that the polarizers are crossed to produce a dark field, the polariscope is then described as a circular dark-field polariscope. Referring to the photoelastic equation given previously

the observed intensity is given by

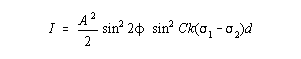
Both of these equations refer to a linear polariscope; if quarter-wave plates are now inserted, the first sine term vanishes (refer to discussion in Dally and Riley, Experimental Stress Analysis, pp. 441-442.) and the intensity is given by

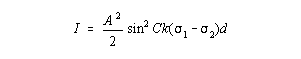
Thus the effect of the quarter-wave plate is to remove the isoclinic lines, leaving the isochromatics unchanged. Another benefit of using quarter-wave plates is that they allow the use of interpolation methods such as null-order compensation and Tardy compensation to determine fringe orders more accurately. Specifically, the Tardy compensation method is commonly used to obtain fractional fringe orders to within a few hundredths of a fringe.

Tardy Compensation

A plane polarizer (quarter-wave plates removed physically or optically) is first used to find the directions of the principal stresses at any selected point. The polarizer/analyzer pair are then rotated as a unit until their axes are aligned with the birefringent indicial axes, and the quarter plates are then reinserted with their axes oriented at the usual 45-degree angle with respect to the new polarizer axes. The system is now in the standard circular dark-field polariscope condition. Up to this point the polarizer/analyzer axes have been kept orthogonal to each other; but now the analyzer is rotated separately until one of the fringes moves over the selected point. In rotating the analyzer up to 90 degrees, the polariscope is changing from a dark-field configuration to a light-field configuration. This change will cause a fringe to move a half-order. For rotations a of less that 90 degrees, the ration of a/90 will correspond to a fractional fringe change relative to a half-order. Thus if the angle through which the analyzer has been rotated is divided by 180 degrees, the resulting value a/180 is the fractional order to be assigned to the selected point. Many polariscopes index a half-circle scale in terms of 100 divisions, so that the fractional order can be read off directly from the scale.

Scaling

Finally, it must be specified how the stress values obtained from observing a plastic model under one load can be scaled up to give the proper results for a real prototype under a different load. This is discussed in the textbook on page 99, under section 5.9. Basically, the result is

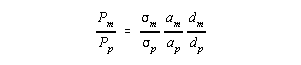
where subscripts m and p refer to model and prototype, P is the load scale factor, s is shearing stress factor, a is the dimensional scale factor, and d is the thickness scale factor.