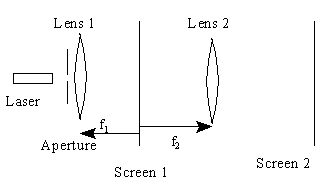
Using the basic principle that the far-field diffraction pattern of light traveling through an aperture is the Fourier transform of the Transmittance function of the aperture, many optical systems have been used to filter an image and clean up noise or otherwise enhance the image.

Recall that the far-field image may be very far away, depending on the size of the aperture. The common equation used to determine approximate values for the location of far-field images is 1/z1 + 1/z2<< l/w2 where w is the characteristic size of the aperture. Generally the input beam is a collimated laser beam, so 1/z1can be set to zero. If w is a small aperture (e.g., 0.01 mm) then z2 need only be a few centimeters away, and no lens is needed. On the other hand, if w is on the scale of 1 cm, then the far-field image will be kilometers away, and then the lens is required to produce the image at a convenient distance.
A key point to remember is that it is the aperture (and its transmittance function) that produces the Fourier transform image. The lens usually found just after the aperture brings the parallel rays that would form the image at a far away distance (check the formula given above) are brought together at the focal plane of the lens.
A second lens placed so that the Fourier transform image is at its focal plane will produce the Fourier transform of the Fourier transform, i.e., the original image will be restored. This may seem like a roundabout method of imaging the original source, but it is a very important technique. The intermediate image is the Fourier transform of the original, and by placing a suitable filter at the location of the intermediate image, many filtering effects can be produced, e.g, high pass filtering, low pass filtering, notch filtering. In determing the frequency effect of the filter, remember that in the Fourier image plane the spatial frequency is given by f = (1/l)(x2/z2).
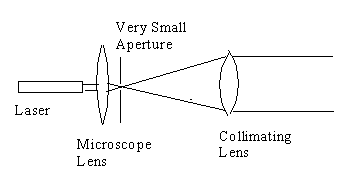
A very common use of Fourier filtering is the spatial filtering frequenty performed on a laser beam to "clean it up" before expanding the beam to a larger size.. Due to dust particles, irregularities in the glass lens cause blotches and irregularities in the expanded beam. To eliminate these defects the beam is first focussed by a microscope lens (short focal length) onto a circular hole of about 25 microns diameter. This small hole acts as a low-pass filter for the Fourier image of the light beam formed by the lens. All of the high frequency noise and ripples are cut off and the output beam from the hole expands into a smooth uniform beam which is then collimated by a suitably chosen second lens.
![]()
Send Comments anytime by e-mail : matthysd@vms.csd.mu.edu
Last Modified on April 20, 1997