Phys 198 February 24, 1997

MIDTERM EXAM

1/f = 1/p + 1/q

m = -q/p

a sin qm = ml

b sin qm= ml

I = Io sinc2(b)

I = Io sinc2(a) sinc2(b)

I = Io [J1(u)/u]2

I = Io [sin(Na)/sin a]2[sinc(b)]2

f = p/2 + q/2

d = moire spacing

tan q = sin f/(d/p + cos f)

p' = pd/(p +/- d)

e = (p' - p)/p

u = Np

exx = du/dx

eyy = dv/dy

gxy = du/dy + dv/dx

s1 - s2 = CN/t

R = C(s1 - s2)t

2tmax = (s1 - s2)

a = (k a sinq)/2

b = (k b sinq)/2

k = 2p/l

fl = v

n = c/v

c = 3 x 108 m/s

  1. In the standard imaging equation 1/f = 1/p + 1/q, under what circumstances will q be negative?
  2. Starting with unpolarized light, how does one produce circularly polarized light?
  3. What is meant by optical retardation and how is it related to birefringence?
  4. What does it mean to optically remove a quarter-wave plate from a polariscope?
  5. What are the different camera requirements for shadow and projection moire?
  6. What are u-field and v-field maps? How would you use them to get gxy ?
  7. What procedural steps are followed to measure partial orders in photoelasticity using the Tardy method?
  8. What is the physical meaning of an isoclinic line in a photoelastic pattern? How can isoclinics be removed?
  9. In the following moire shown in Figure 1 determine the amount of rotation undergone by the sample. (Actually, since you can see the full intersection of the grids, you can directly measure the angle. However, assume that you can only see the central region with the moire and that you know the master grid is 50 mm wide, has a grid density of 2.3 lines/mm, and is aligned with its lines horizontal.. You may also assume there is no strain.)
  10. What is the strain and rotation indicated by the moire shown below in Figure 2? The master grid is 50 mm wide, has a line density of 2.3 lines/mm, and is aligned with its lines horizontal..

Figure 1. Rotated grids with no strain.

Rotation Only Grids


















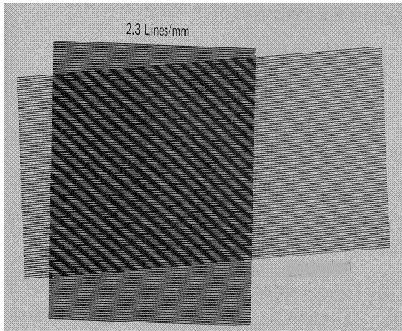
Figure 2. Moire from rotation and uniform strain.

Rotation and Strain moire

















 

Return to Physics 198 Main Page Return to Matthys' Home Page
Last Modified on April 20, 1997