May 1, 2001
[Open book exam, but no consultation with fellow students. Printed copy
of your answers is due in Fr. Matthys' mailbox (Physics office on 3rd floor) by
5:00 pm on Thursday, May 9, 2001. Note that the images in the exam are not
thumbnails.]
1. An image has six different data values, a2, a6,
a1, a4, a3, a5, with respective
probabilities of 0.4, 0.3, 0.1, 0.1 0.06, 0.04. Calculate the Huffman
codes for this array. What are the data values in the encoded string
010100111100 ?
2. In the picture below, display bitplane 6.
Manipulate the image to obtain the Gray code version of bitplane 6.

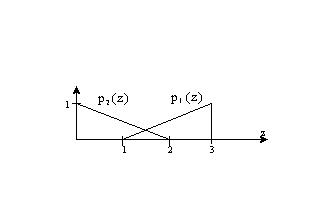
3. Suppose that an image has the following intensity
distributions, where p1(z) corresponds to the intensity of
foreground objects and p2(z) corresponds to the intensity of
the background. Assume that P1 = P2
and find the optimal threshold between object and background pixels.
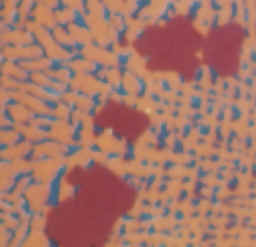
4. The picture below shows a three-phase (three color)
metallographic image. Use color filtering and/or thresholding to determine
the relative areas of the three phases.
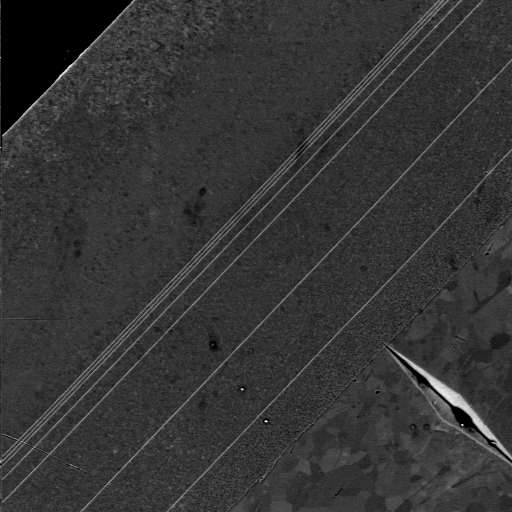
5. The picture below is a calibration specimen for SEM (scanning
electron microscope) images. The two outside lines of the seven thin
parallel lines are 50 microns apart. a) What is the distance between
the two most widely separated adjacent lines? b) Counting from the side where
the lines are close together, what is the distance between line 1 and line
3? c) Use FFT techniques to i) remove the set of lines from the
image while leaving the rest of the picture, and then ii) enhance and sharpen
the lines while removing almost everything else.
6. Starting with the picture below of two birds, compose
two color pictures with a flat background, each containing a different
bird. Don't worry too much about edge effects.

