|
Feb 14, 2001
Lab 2
Laplacian filters are derivative filters used to find areas of rapid change
(edges) in images. Since derivative filters are very sensitive to noise, it is
common to smooth the image (e.g., using a Gaussian filter) before applying the
Laplacian. This two-step process is call the Laplacian of Gaussian (LoG)
operation.
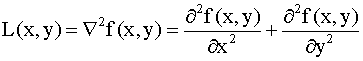
There are different ways to find an approximate discrete convolution kernal
that approximates the effect of the Laplacian. A possible kernel is
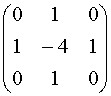
This is called a negative Laplacian because the central peak is negative. It
is just as appropriate to reverse the signs of the elements, using -1s and a +4,
to get a positive Laplacian. It doesn't matter.
To include a smoothing Gaussian filter, combine the Laplacian and Gaussian
functions to obtain a single equation:
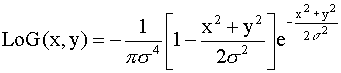
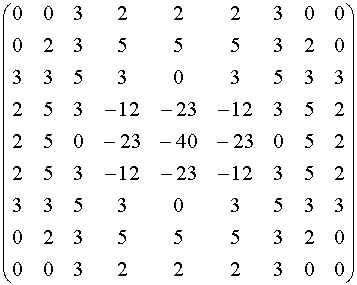
A discrete kernel for the case of σ = 1.4
is given by
The LoG operator takes the second derivative of the image. Where the image is
basically uniform, the LoG will give zero. Wherever a change occurs, the LoG
will give a positive response on the darker side and a negative response on the
lighter side. At a sharp edge between two regions, the response will be
 | zero away from the edge |
 | positive just to one side |
 | negative just to the other side |
 | zero at some point in between on the edge itself |
When using the filter given above, or any other similar filter, the output
can contain values that are quite large and may be negative, so it is important
to use an image type that supports negatives and a large range, and then scale
the output. (ImageJ has a 32-bit floating point representation). Alternatively,
a scaling factor can be used on the filter to restrict the range of values.
Generate a LoG filter with Gaussian σ =
1.0, using a 7x7 kernel. Apply this filter to the image given below.
.

What can you say about the output image? Now
combine (subtract) the two images in an effort to sharpen the original image.
You may have to scale the filtered image before combining the two images. Also,
you may have to translate the filtered image by half the width of the
convolution kernel in both the x and y directions in order to
register the images correctly. A little experimentation may be required. Save
the result you think is your best effort
The enhancement sharpens the edges but also increases noise. If the original
image is filtered with a simple Laplacian (a LoG filter with a very narrow
Gaussian), the resulting output is rather noisy. Combining this output with the
original will give a noisy result. On the other hand, using a larger σ
for the Gaussian will reduce the noise, but the sharpening effect will be
reduced. Life is full of compromises.
Last modified on March 21, 2001
| 