Problem Set 2:
1. Show that the discrete Fourier transform and its inverse are
periodic functions. Assume 1-dimensional functions.
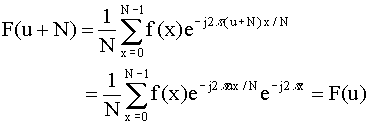
since exp(-j2πx)= 1 for all integer x.
2. Show the validity of the translation properties of the discrete
2-dimensional Fourier transform pair. Show the translation properties for
the special case of a square image when wo = zo = N/2.
f(x,y)exp[j2πwox + zoy)/N] ó
F(w - wo, z - zo)
is easily shown by just substituting w+wo, etc, in the defined exponential
kernal for the Fourier transform and its inverse. For the special case wo
= zo = N/2
Substitute wo = N/2 and recall that exp[-j2π(N/2)x/N] = exp[-jπx]
is +1 for even x and -1 for odd x; same is true for zo = N/2 and the
y values. So plugging in these values for the exponential exp[-jπ(x+y)]
gives (-1)x+y. Therefore multiplying the original images values by
(-1)x+y will center the spectrum in Fourier space.
3. A one-dimensional function f(x) is sampled at four points: xo
= 0.5, x1 = 0.75, x2 = 1.0, and x3 = 1.25,
producing data values f(x) at those points of 2, 3, 4, 4, respectively.
Calculate the Fourier transform, and determine the Fourier spectrum.
Here N = 4, and x(0) = 2, x(1) = 3, x(2) = 4, and x(3) = 4.
