Apr 23, 2001

Standard n-bit binary coding: 000 001 010 011 100 101 110 111 (n = 3)

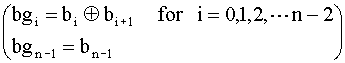
Compression ratio: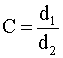

Redundancy:

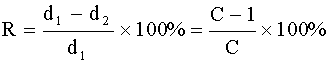
Histogram: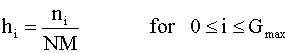

Average bits per graylevel: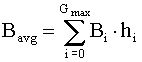

Entropy: 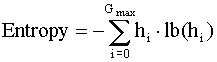                     (units are number of bits)

· Coding : want to minimize average bits per graylevel
· Spatial : exploit correlation between neighboring pixel values
· Visual : human eye limitations as applied to image data

 

Compression can be either error-free or lossy.

Coding: Huffman, error-free and near optimal, but uses complex algorithm.

Example for image of 8 greylevels:

This image has an entropy of 2.55 bits/pixel.

Applying Huffman coding to this data gives the coding representation:

The average bits/pixel for the compressed image is 2.59, slightly larger than the entropy of 2.55.  Huffman coding compared to straight 3-bit binary coding has given a compression ratio of 1.16:1 or a 14% reduction in size.

Another example showing how to decode the Huffman representation:

Original Huffman Code: 110011000010000111
Greylevels: g_o,g₃,g₂,g₅,g₇.

Arithmetic coding of a binary sequence is covered in the text.

Run Length coding: If pixel values are correlated to their neighbors, then there will be sequences of the same value. Instead of coding all the repeat values, just encode the first value and then give the run length of the sequence.

Bit-plane coding: break image up into bit planes and apply run length coding to each plane.

To get the bit planes of the above 8-bit grayscale image, AND the picture with the binary value corresponding to the desired plane; i.e., ANDing the image with 10000000 should give the 7^th bit plane, ANDing the image with 00100000 should give the 5^th bit plane, etc. After the AND operation, use the thresholding operation to make a binary image. It may also be necessary to invert the result.

Last modified on April 25, 2001