|
Phys 4, Section 2
Feb 13, 2002
Magnetism (Permanent Magnets)
Magnetism: first noticed as effect of iron ores by Greeks in Magnesia.
Magnetic Poles: always N and S in a pair, never a separate monopole.
Use of Magnet as compass
Magnetic Field
Magnetic field B is caused by moving charge (current); this field is
experienced by other moving charges.
F = qυ × B (Units
of B are Tesla: 1 T = 1 N/A · m; also gauss: 1 G = 10-4 T)
Lorentz Force: F = q(E + υ
× B)
Magnetic Field Lines and Magnetic Flux
Field lines come out of N poles and go into S poles, except within the magnet
itself where the lines go from S to N. Magnetic field lines have no origination
or destination points, but always form closed loops.
Magnetic flux is defined: 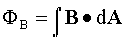
Gauss' Law for Magnetism: 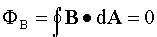
Charged Particles in B
Magnetic force F is at right angles to motion υ
of charged particle q, so does no work, but can only change
direction of motion, it acts as a centripetal force driving the particle in
circular motion of radius R:
F = qυB = mυ2/R
but
ω = υ/R
so get ω = qB/m (cyclotron frequency).
Crossed B and E fields (balance of E-force and B-force):
velocity selector: υ = E/B
Thomson's e/m experiment: mv2/2 = eV → e/m
= E2/2VB2
Magnetic Force on current-carrying conductor of length L:
F = IL × B
Last modified on February 27, 2002
|