RC Circuits
Home Electrostatics Coulomb's Law Electric Field Gauss's Law Electric Potential Energy Electric Potential Capacitors Energy in Capacitors Current Electrical Power and Resistors Kirchhoff's Rules RC Circuits Magnetic Fields Moving Charges in a B-Field Magnetic Field of a Moving Charge Magnetic Field Due to a Current Ampere's Law

 

Procedures
Lectures
Quizzes
Exams
Assignments
MidTerm
Final

Phys 4, Section 2                                                                 Feb 11, 2002

 

Time Constant for RC Circuits

 

RC Circuits:

Given a resistor R and a capacitor C in a series circuit, what happens when a battery of voltage Vo is placed across the circuit?

Charging a capacitor:

The voltage drop across the resistor is iR while the voltage drop across the capacitor is q/C. If these voltage drops are used in a Kirchhoff's loop around the circuit

Vo -iR - q/C = 0

Now using the relation i = dq/dt, the equation for charging the capacitor is

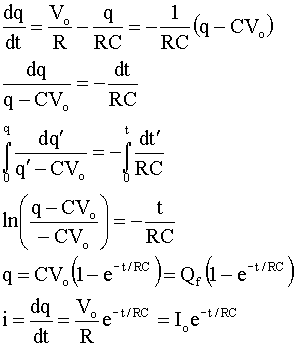
The value RC is called the time constant τ = RC and is measured in seconds. One time constant is the time required for the current to reach 1/e (about 1/3) of its initial value. After 5 time constants, the current has decayed to 1% of its initial value.

Discharging a Capacitor

Assume that many time constants have gone by and the capacitor is essentially charged to the same voltage as the battery Vo, the charge q on the capacitor is Qo, and the current I is zero. Remove the battery and short circuit the terminals of the RC circuit. What does Kirchhoff say about the voltage across the capacitor or the current in the resistor?

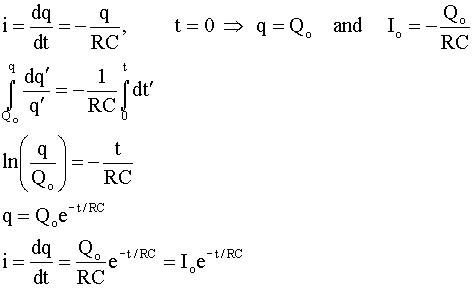
Magnetic Fields

Magnetism first studied by Greeks in Magnesia through phenomenon of permanent magnets. Used for navigation, needle shaped magnets had one end which pointed North and one end which pointed South. Magnets interacted much as charges did, with likes repelling and opposites attracting. Magnetic forces are due to moving charges.

The force between electric charges are described by an electric field E. So too the forces between magnets can be described by a magnetic field B. A major difference however is that an electric charge always produces an E-field, while a B-field is only associated with a charge when the charge is moving.

F = qv × B

From this equation, the units of the magnetic field are N/(A٠m), or in teslas.

1 T = 1 N/(A٠m) Another common unit (cgs) is a gauss (1 G = 10-4 T)

The magnetic field has field lines and flux just like the electric field, however, since there are no separated magnetic poles (N and S) as there are charges (+ and -), Gauss's law for magnetic flux through a closed surface is different:

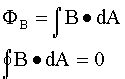
Note that the unit of magnetic flux is a weber (Wb): 1Wb = 1 T٠m2 = 1 N٠m/A

 

Last modified on February 11, 2002