Phys 4, Section 1                                                             Jan 25, 2002

If forces act, then work can be done; if work is done there may be changes in kinetic energy and potential energy. Note that the electric force is conservative; only when we treat resistance in circuits will we have to worry about losses.

W = ∫F•ds

If the force is conservative, the work W can be expressed in terms of potential energy U :

W_ab = -ΔU_ab

Also, note that for conservative forces, the total mechanical energy K + U is constant. Note that W is work done by the system, not work done on the system by external forces.

For charge q_o in a uniform field E moving a distance d in the direction of E:

W = Fd = q_oEd

The change ΔU is -q_oEd since W = -ΔU

F = kqq_o/r²

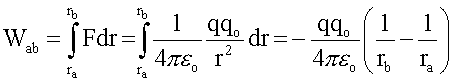
Let r_a be at infinity and define the potential energy between charges to be zero for infinite separation. Then for any charge q_o located at distance r from charge q, the electric potential energy is

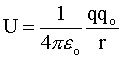
Last modified on January 31, 2002