|
Phys 4, Section
2
Feb 25, 2002
Ampere's Law
For a closed loop of perimeter L with a current I enclosed in
the loop, Ampere's law asserts:
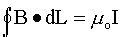
Displacement Current
Ampere's Law as given above fails when applied to a circuit with a charging
capacitor. Recall that C = Q/V and for a flat-plate capacitor, C = eoA/d.
Using q, v and i for instantaneous values of charge,
potential and current, respectively,
q = Cv = (eoA/d)(Ed) = eoEA = eoFE,
with FE representing the electric flux. Since i = dq/dt,
then
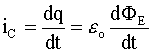
is an expression for the current flowing into the capacitor. This expression was
extended by James Maxwell to cover the displacement current
flowing through the empty space between the capacitor plates. Note that this
displacement current does not involve the motion of charge, but rather the rate
of change of an E-field. Note also that the displacement current between
the plates is equal to the real current of moving charge flowing into the
capacitor. Maxwell extended Ampere's law to include displacement currents:
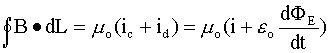
Note that since Φ = ∫ E•dA
, a displacement current density jD = iD/A can be
defined as:
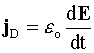
Last modified on February 27, 2002
|