Moving Charges in a B-Field
Home Electrostatics Coulomb's Law Electric Field Gauss's Law Electric Potential Energy Electric Potential Capacitors Energy in Capacitors Current Electrical Power and Resistors Kirchhoff's Rules RC Circuits Magnetic Fields Moving Charges in a B-Field Magnetic Field of a Moving Charge Magnetic Field Due to a Current Ampere's Law

 

Procedures
Lectures
Quizzes
Exams
Assignments
MidTerm
Final

Phys 4, Section 2                                                         Feb 18, 2002

 

 

 

Motion of Charged Particles in a B-Field

Since magnetic force FB is perpendicular to direction of motion v, no work is done and no change in magnitude of velocity vector is possible, only change in direction. If the force and velocity are constant and at right angles, the particle will go in a circle of radius R, and the magnetic force FB will act as a centripetal force FC:

           

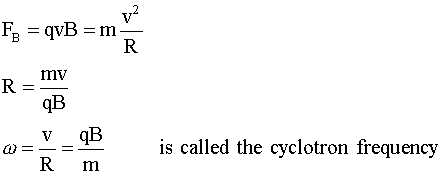
Velocity Selector

If a moving charged particle is placed between crossed E and B fields, it will feel two forces, electric and magnetic. If the fields are properly oriented, there is a unique velocity at which the forces will cancel and the particle will move at constant speed in a straight line.

           

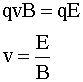
Magnetic Force on a Current-Carrying Conductor

Let density of free charges moving with drift velocity vd in a conductor be n; then a segment of length L and cross-section A will have nAL charges. The total force on all these charges due to a B-field oriented perpendicular to the conductor is

            J = nqvd and JA = I, so

            F = ILB

In the more general case where the conductor and B-field are not perpendicular to each other,

            F = ILB sin φ

              F = IL × B

where φ is the angle between conductor and field

Force and Torque on a Current Loop

A rectangular loop of dimensions a and b, carrying a current I, and free to rotate about a central axis passing through the midpoints of b on opposite sides plane of the loop is placed in a uniform B-field which is perpendicular to the loop axis. Calculating the force on each side of the loop shows that the forces on opposite sides of the loop cancel, so there is no net force. However, since the loop can rotate about its axis, torques must be considered.

            τ = 2F(b/2)sin φ = IBab sin φ = IAB sin φ

if the product of the loop area A and the current I around the loop is called the magnetic dipole moment μ, then the torque can be described as

            τ = μ × B

A special case is that of a solenoid, which consists of many (N) closely wound loops. The total torque on all the loops is given by

            τ = NIAB sin φ

where φ is the angle between the solenoid axis and the B-field.

 

 

Last modified on February 27, 2002