Jan 22, 2001

If have periodic function f(x), it can be expressed as a Fourier series:

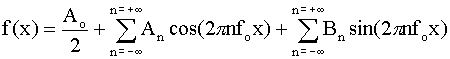
where can get the coefficients:

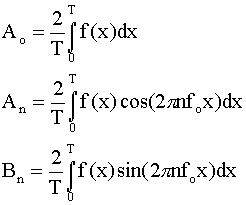
by using the fact that the sines and cosines are orthogonal over their periods.

If the function f(x) is not periodic, then have to use the integral form:

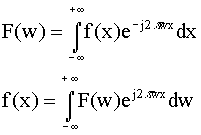
which are called a Fourier transform pair. Notice that in this case all frequencies are present in the transform, not just the harmonic frequencies found in the Fourier series.

f(x) is usually a real function, but F(w) is complex. F(w) can be expressed in terms of a real and an imaginary part, and also as having magnitude and phase components.

Because the range of  |F(w)| is generally very large, the display of |F(w)| on a monitor usually is transformed to show: D(w) = log(|F(w)| + 1).

Generally, when using Fourier transforms for image processing, have to use finite sampled series. Discrete sampled forms of the Fourier transforms can be obtained by applying the point, pulse, and comb functions:

Point: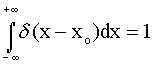

Pulse: rect(x/a) = 1 for , 0 otherwise

Comb:

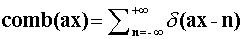
Start with a continuous f(x) that is bandwidth limited, get F(w).

Sample f(x) using the comb function with a spacing of a, this will make F(w) periodic.

Truncate the sampled data to N samples by using the rect function, this will extend lobes on F(w) from sinc function effect.

Sample F(w) using the comb function with a spacing of 1/a, this will make f(x) periodic.

Two-Dimensional Fourier Transform

In two dimensions, the Fourier transform pair is expressed as

Last modified on January 24, 2001