Lossy Compression

 

Home
Image Fundamentals
Fourier Transforms
Fourier Properties
Point Operations
More Point Operations
Spatial Filters
Frequency Filters
Image Restoration
Frequency Filters
Homomorphic Filters
Color Models
Color Palettes
Color Processing
Image Geometry
Image Compression
Run Length Encoding
Lossy Compression

Apr 30, 2001

Lossy Methods
Predictive coding and transform coding

Predictive coding:

Difference between error free and lossy methods is the presence of a quantizer.

            fe(x,y) = q(x,y) + fest(x,y)

and

            e(x,y) = f(x,y) - fest(x,y)

For one-bit binary delta quantizer:

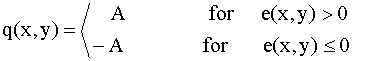
A small value of A causes slope overload, while a large value causes granular noise. Thus the choice of A must always represent a compromise.

If the predictor is the common fest(x,y) = f(x-1, y) and A = 1
 then the following table can be generated for a specific example (in one dimension) 1,1,1,2,6,6,5,4,4,4, assuming the initial value for the predictor in both the encoder and the decoder is 1:

Encoder

Decoder

f(x)

fest(x)

e(x)

fe(x)

q(x)

fest(x)

fi(x)

1

-

-

1

-

-

1

1

1

0

0

-1

1

0

1

0

1

1

1

0

1

2

1

1

2

1

1

2

6

2

4

3

1

2

3

6

3

3

4

1

3

4

5

4

1

5

1

4

5

4

5

-1

4

-1

5

4

4

4

0

3

-1

4

3

4

3

1

4

1

3

4

 

The errors are the result of the quantization of the error function e(x,y). This function is usually a sharp peak around zero, but if want to cover all possible errors, then the value of the error must be quantized into many bits, which reduces the compression possibilities. It is in allowing the less likely error values to go unrecorded that large compression values are obtained. Usually a scheme is used where a small number of bits are used to code error values near the peak of zero while larger numbers of bits are used for values farther from the peak.

Transform Coding:

By far, the most popular transform for image compression is the DCT  Indeed, the DCT is the basis of the JPEG international standard for color image compression. The big advantage of the DCT over the DFT is the assumed periodicity. The assumed periodicity for the DFT is N (NxN image) and if the actual image has different values on opposing sides, ringing effects and high order coefficients are introduced. This creates objectionable edge effects in the final image. However, the DCT assumes mirror symmetry over a period of 2N (NxN image) so at each edge the value is assumed to be continuous. Thus there is almost no ringing and the higher order coefficients are negligible.

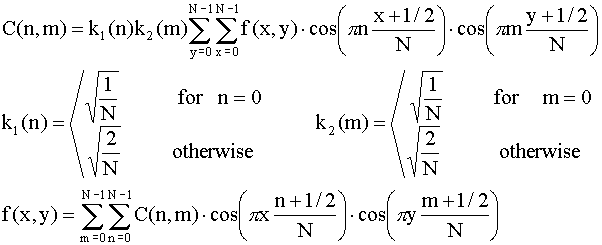
A cutoff is determined by rejecting all coefficients below a chosen threshold or by rejecting all coefficients above a certain frequency. This truncation allows considerable compression.

 

Last modified on April 30, 2001