Fourier Properties

 

Home
Image Fundamentals
Fourier Transforms
Fourier Properties
Point Operations
More Point Operations
Spatial Filters
Frequency Filters
Image Restoration
Frequency Filters
Homomorphic Filters
Color Models
Color Palettes
Color Processing
Image Geometry
Image Compression
Run Length Encoding
Lossy Compression

Jan 24, 2001

Discrete Fourier Transforms

 

The discrete Fourier transform pair for a sampled space array f(x, y) of dimensions M x N to a frequency array F(w, z):

                   

 

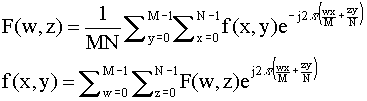
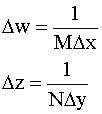
Properties of two-dimensional Fourier transform (assume M=N):

Commutivity:
            [af(x,y) + bg(x,y)] ó aF(w,z) + bG(w,z)
Translation:
            f(x, y) exp[j2π(wox + zoy)/N] F(w - wo, z - zo)
            f(x - xo, y - yo) F(w, z) exp[-j2π(wxo + zyo)/N]
  Periodicity:
            F(w,z) = F(w+N, z) = F(w, z+N) = F(w+N, z+N)
Rotation:
            Let x = r cos θ, y = r sin θ, w = ρ cos φ, z = ρ sin φ
            Then     f(r, θ + θo) ó F(ρ, φ + θo)
Scaling:
            a f(x, y) ó a F(w, z)
            f(ax, by) ó (1/|ab|)F(w/a, z/b)

The Fourier transform of a constant valued image  is a delta function located at (0,0) and multiplied by the constant value.

f(x,y) ó Aδ(m,n)

The comb function preserves its form under a Fourier transform:

       

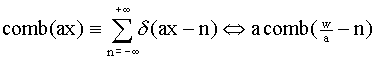
Convolution


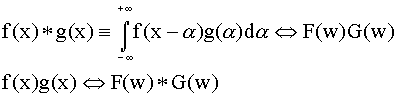
A basic reason for the importance of the Fourier transform is that it allows the mathematical complexity of a convolution integral to be replaced by the product of Fourier transforms. 

 

Do Homework Assignment 2.

 

Last modified on January 29, 2001