Image Geometry

 

Home
Image Fundamentals
Fourier Transforms
Fourier Properties
Point Operations
More Point Operations
Spatial Filters
Frequency Filters
Image Restoration
Frequency Filters
Homomorphic Filters
Color Models
Color Palettes
Color Processing
Image Geometry
Image Compression
Run Length Encoding
Lossy Compression

Mar 12, 2001

 

Image Mapping

In changing the size or orientation of an image, it is frequently necessary to interpolate pixel values. For example, if it is desired to change an NxN image to a 2Nx2N image, no one-to-one mapping is possible, and some method of choosing the values of the inserted pixels must be determined.

· Replication by nearest neighbor
· Linear interpolation
· Spline interpolation (usually cubic spline)

Linear Image Translation and Rotation

The geometrical result of translating, rotating, and scaling an image can be handled by linear algebra methods. Restricting the discussion to two dimensions:

Translation:

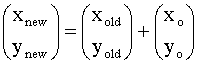will translate a pixel by (xo, yo)

Rotation:

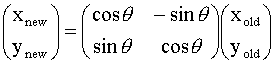rotates a pixel by q about the origin (0, 0)

Scaling:

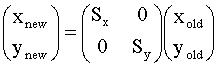scales an image in x and y directions by Sx and Sy.

If negative scaling factors are used, the new image will be flipped about the axis with the negative scaling factor.


Last modified on February 28, 2001