Feb 19, 2001

The Fourier transform is linear and associative under addition, but is not associative under multiplication. Thus, Fourier methods are suitable for removing noise from images only when the noise can be modeled as as additive term to the original image.

However, if defects of the image, e.g., uneven lighting, have to be modeled as multiplicative rather than additive, direct application of Fourier methods is inappropriate.

In terms of the illuminance and reflectance of an object, an image of the object might be modeled as f(x,y) = i(x,y)·r(x,y). In this case, some way of converting multiplication into addition must be employed before trying to apply Fourier filtering. The obvious way to do this is to take logarithms of both sides:

q(x,y) = ln[r(x,y)·i(x,y) + 1] = ln[i(x,y)] + ln[r(x,y)]

where 1 has been added to the image values to avoid problems with ln[0].

Taking the FFT of both sides

Q(n,m) = I'(n,m) + R'(n,m)

where n and m are spatial frequencies in the x and y directions

Now apply a suitable Fourier filter function H(n,m)

S(n,m) = QH = I'H + R'H

where I'(n,m) is the Fourier transform of ln[i(x,y)].  

Now take inverse FFT

s(x,y) = ln[r(x,y)] + ln[i(x,y)]

Finally, take the exponential of both sides, and subtract the extra 1 from each pixel:

g(x,y) = exp[s(x,y)] - 1 = r(x,y)

Examples of poor illumination:

Generation of Spatial Masks

In the frequency domain,

G(u,v) = H(u,v)F(u,v)

produces the Fourier transform of a filtered image, where H represents the frequency filter.  How can the spatial mask h(x,y) equivalent to H(u,v) be obtained?

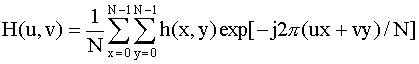
for u,v = 0, 1, 2, …, N-1.  But for an  n×n convolution mask 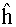with n < N, 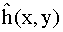must be zero for x > n and y > n.

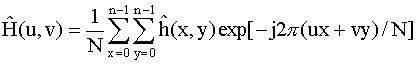
for u,v = 0, 1, 2, …, N-1.

How can minimization, in the least-squares sense, be achieved for the error

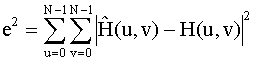
In matrix form,

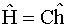
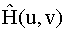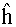where is a column vector of order N² containing the elements of ,  is a column vector of order n² containing the elements of 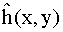, and C is an N² × n² matrix of exponential terms.  A simple way to order the terms is to let 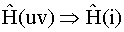, where i = uN + v in row order.  Similarly, 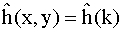, for k = xn + y.  Finally, C = C(i,k) is generated from

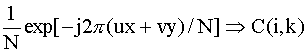
for i = uN + v, and k = xn + y, all in row order.

Putting all this in matrix notation

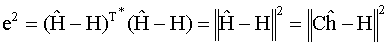
Setting the partial derivative equal to zero yields the minimum of e².

Then

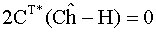
giving as a final answer:

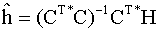
which gives the coefficients to construct an n×n convolution mask 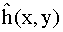from a specified N×N frequency filter H(u,v).  In general, the elements of 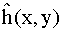would be complex, but if the frequency domain filter is real and symmetric, 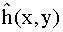is also real and symmetric.

Last modified on February 21, 2001