Feb 14, 2001
Frequency filters
Filters in general can be lowpass, highpass, bandpass,
and notch. Ideal filters have sharp edges and discontinuities and
so introduce ringing into image filtering. There are however, several filters
that are continuous at the expense of having a gradual instead of a sharp cutoff
at some desired frequency (or frequencies).
Gaussian lowpass:
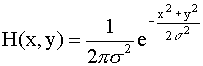
This is a zero mean Gaussian with standard deviation σ.
The normalization constant is frequently ignored in discrete masks, since there
are other factors, such as the range of values and the overall normalization of
mask constants, that tend to take precendence.
There is only one variable in the Gaussian, its standard deviation. To get
more flexibility, a more flexible filter, the Butterworth, is frequently used.
Unlike the Gaussian, the Butterworth comes in two flavors
Butterworth:
Lowpass:
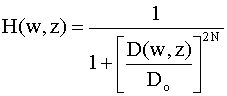
Highpass:
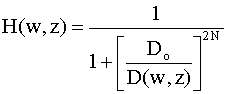

Image Restoration
If an image f(x,y) is degraded going through an optical system and the
detected image g(x,y) represents the effect of the point function h(x,y) of the
system, then in the frequency domain the process can be represented by G = HF,
where it is assumed that there is no noise. If it is further assumed that H(w,z)
is either known or can be determined, then it is possible to regain the original
image by the process
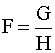
All of this work is done in the frequency domain and the result Fourier
transformed back to real space. The idea is good, however, this process is
very susceptible to noise (although a more complicated effort using Wiener
filters might help if there is noise) and demands very accurate knowledge of
the transfer function H.
Last modified on February 14, 2001
