Jan 29, 2001

Enhancement by Point Operations

A point operation is a modification to a pixel value which is based on that pixel value and is independent of location or neighboring values.

Point operations can be applied by

Value substitution from a LUT can change brightness and contrast

Addition of pixels from multiple images can average out noise

Subtraction of images can remove background variations and highlight change

Multiplication of images can be used to compensate for camera variations

Look Up Tables (LUTs)

Brightness is defined:

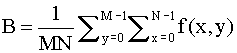
Contrast is defined:

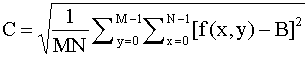
A LUT is used to map a set of input values to a set of output values. For 8-bit grayscale images, there are usually 256 possible values for input or output. If r is an input value and s is an output value, then

s = T(r) where T(r) is a monotonic mapping function between r and s.

For an N x M image

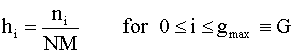
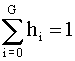
To get average value of pixels in image:

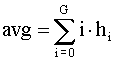
Histogram equalization is an attempt to distribute the gray levels of an image evenly over the maximum possible range.

It is obtained by obtaining the cumulative probability distribution of r, solving this for r in terms of s, and using this for the mapping function T(r).

The probability density function for the s values is given by

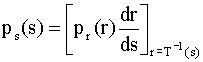
The cumulative distribution function of r is obtained by

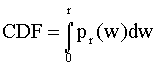
Using this distribution function for T(r) gives

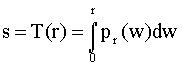
which will have a uniform density.

Example of Histogram Equalization

As an example consider the probability distribution function for r given by p_r(r) = -2r+2 for r = [0,1]

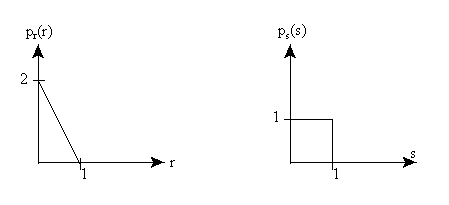
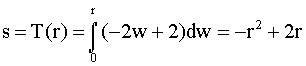
then

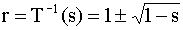
where only the minus value is valid, since r ≤ 1

This will give a uniform density for the probability density function of s:

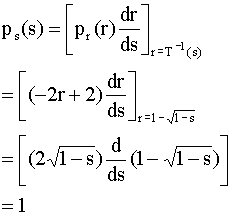
for 0 ≤ s ≤ 1.